自然语言处理：最大熵和对数线性模型
Natural Language Processing: Maximum Entropy and Log-linear Models 作者：Regina Barzilay（MIT,EECS Department, October 1, 2004)译者：（ ，2009年4月29日）一、 词性标注（POS tagging）：
c) 特征向量表示（Feature Vector Representation） i. 一个特征就是一个函数f（A feature is a function f ）：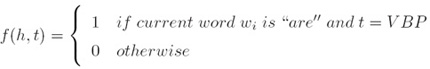
ii. 我们有m个特征fk，k = 1…m（We have m features fk for k =1…m）d) 词性表示（POS Representation） i. 对于所有的单纯/标记对的单词/标记特征，（Word/tag features for all word/tag pairs）：
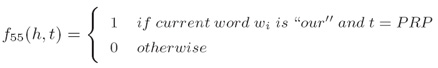ii. 对于所有特定长度的前缀/后缀的拼写特征（Spelling features for all prefixes/suffixes of certain length）：
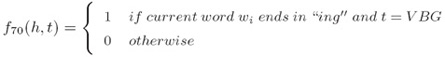iii. 上下文特征（Contextual features）：
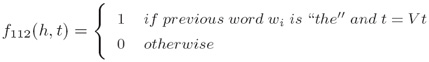iv. 对于一个给定的“历史”x ∈ X ，每一个γ中的标记都被映射到一个不同的特征向量（For a given history x ∈ X, each label in γ is mapped to a different feature vector）：
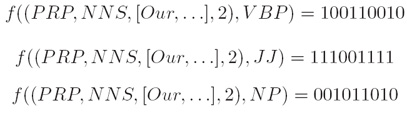v. 目标（Goal）：学习一个条件概率P(tag|history)（learn a conditional probability P(tag|history) 二、 最大熵（Maximum Entropy）：
a) 例子（Motivating Example）： i. 给定约束条件：p(x, 0)+p(y, 0)=0.6，a ∈{x, y}且b ∈0, 1，估计概率分布p(a, b)（Estimate probability distribution p(a, b), given the constraint: p(x, 0) + p(y, 0) =0.6, where a ∈{x, y}and b ∈0, 1））：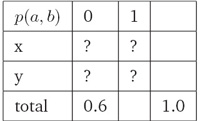
ii. 满足约束条件的一种分布（One Way To Satisfy Constraints）： 
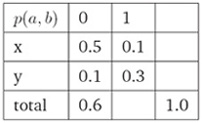iii. 满足约束条件的另一种分布（Another Way To Satisfy Constraints）： 
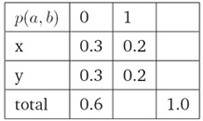b) 最大熵模型(Maximum Entropy Modeling) i. 给定一个训练样本集，我们希望寻找一个分布符合如下两个条件(Given a set of training examples, we wish to find a distribution which)： 1. 满足已知的约束条件（satisfies the input constraints） 2. 最大化其不确定性（maximizes the uncertainty） ii. 补充： 最大熵原理是在1957 年由E.T.Jaynes 提出的，其主要思想是，在只掌握关于未知分布的部分知识时，应该选取符合这些知识但熵值最大的概率分布。因为在这种情况下，符合已知知识的概率分布可能不止一个。我们知道，熵定义的实际上是一个随机变量的不确定性，熵最大的时侯，说明随机变量最不确定，换句话说，也就是随机变量最随机，对其行为做准确预测最困难。从这个意义上讲，那么最大熵原理的实质就是，在已知部分知识的前提下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断，这是我们可以作出的唯一不偏不倚的选择，任何其它的选择都意味着我们增加了其它的约束和假设，这些约束和假设根据我们掌握的信息无法做出。（这一段转自北大常宝宝老师的《自然语言处理的最大熵模型》）
附：课程及课件pdf下载地址：
http://people.csail.mit.edu/regina/6881/